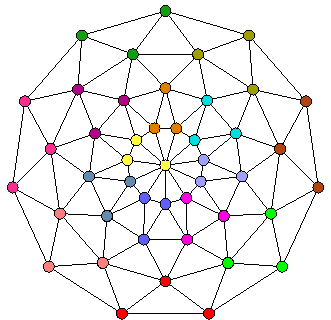
The library comes with several constructor methods which grow graph objects from one or more numeric input parameters:
- regularTree : Rooted trees where all non-leaf nodes have a specified degree. Either with a specified depth or a specified number of nodes
- sierpinskiTriangle : Recursive construction of a series of planar, nearly 4-regular graphs
- openGrid : Tessilations of the Euclidan plane with regular faces (either triangles, squares or hexagons), truncated to a specified grid size
- polarGrid : Radial grids with 0, 1 or two poles and triangular or quadrilateral faces. Useful for the construction of regular polyhedra (see Section Planar composition )
- toroidalGrid : Similar to the openGrid construction. Wrap-around in replace of truncation, to preserve the node regularity. These graphs are non-planar, but can be embedded on a torus surface
- moebiusLadder : A series of non-planar graphs which can be embedded on a projective plane
- gridCompletion : Similar to the openGrid construction, but here all pairs of nodes on a grid line are adjacent. The input parameter denotes the maximum clique sizes
- triangularGraph : Graphs on the 2-element subsets of a ground set with specified cardinality. Non-planar, node regular
- permutationGraph : Graphs on a given node set, and an optional permutation. Special case of comparabilty graphs and, by that, of perfect graphs
- thresholdGraph : Graphs on a given node set, a threshold value for edge weights, and optional node weights. Special case of chordal and, by that, perfect graphs
- intervalGraph : Intersection graphs on a given node set, and optional node intervals. Special case of chordal and, by that, perfect graphs
- mycielskianGraph : A series of graphs with growing chromatic number, but constant clique number 2
- butterflyGraph : A series of layered graphs
- cyclicButterfly : A series of regular digraphs with a cyclic layering
These classes apply as test cases for optimization and drawing methods, in particular when used as a seed for the composition principles which follow, and the randomization procedures described in Section Random manipulations.
Except for the triangular and the Mycielskian graphs (which do not admit readable drawings), all constructor methods provide the expectable geometric embeddings.
[See API]
What follows is a list of well-known principles to construct graph objects from other graphs:
- complementaryGraph : A node pair is adjacent if it is non-adjacent in the original graph
- lineGraph : Defined on the edge set of the original graph. Edged are adjacent if sharing an end point
- colourContraction : Identify all equally coloured nodes
- explicitSurfaceGraph : Identify nodes in the same toplevel set of a specified nestedFamily
- completeOrientation : Split each undirected edge of the original graph into a paair of anti-paralllel arcs
- inducedOrientation : Orient the edges such that colour indices are increasing from arc tails to head nodes
- nodeSplitting : Break each node into a pair of nodes, joined by an arc which has the original node demand as its upper capacity bound
- inducedSubgraph : The subgraph induced by a node index set and, optionally, an edge index set
- inducedBigraph : The bipartite subgraph induced by two node index sets
Other than the methods discussed further on, the constructors listed here work for general graph objects.
[See API]
The library provides several methods to generate planar graphs from other planar graphs. It is required that the original graph comes with a planar representation, and the new graph is generated with a respective planar representation. The composition methods generalize from construction principles for regular polyhedra.
Most important is the dualGraph construction. This takes the original regions as the node set, connecting nodes if the original faces share an edge. Actually, the edges are mapped one-to-one. The directedDual constructor works similar but assigns arc orientations acoording to the orientation of the original arc.
Observe that the dual of the dual is basically the original graph, provided that the graph is connected. In the directed case, the arc orientations are reverted.
A potential drawing of the original graph is mapped, but the quality of the resulting drawing is currently limited by the dual node representing the exterior face of the original graph (A special treatment of infinite nodes is missing). The following shows an outer-planar graph and its dual graph, with the exterior face displayed in the center:
Other constructors (vertexTruncation and planarLineGraph) replace the original nodes by faces. The constructor facetSeparation maintains the original faces and duplicates the original nodes for every adjacent face. Observe that all constructors yield node-regular graphs:
In order to obtain the full set of Platonian and Archimedian polyhedra, the constructor method polarGrid comes into play which is very flexible:
- The tetrahedron is a polar grid with 1 rows, 3 columns and 1 pole
- The octahedron is a polar grid with 1 rows, 4 columns and 2 poles
- The icosahedron is a polar grid with 2 rows, 4 columns, triangular faces and 2 poles
- The dodekahedron is the dual of an icosahedron
- Prisms are polar grids with 2 rows, square faces and no poles (and the cube the prism with 4 columns)
- Antiprisms are polar grids with 2 rows, triangular faces and no poles
The following shows a polar grid with 4 rows, 11 columns and a single pole (to obtain this drawing, polarGrid::POLAR_CONE must be specified):
[See API]
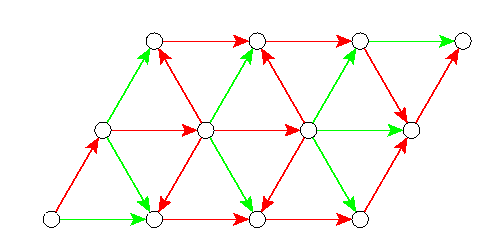
In a directed graph, the arc set can be considered a relation of the graph nodes. According to that, the transitive closure of a digraph is the digraph with the same node set and with arcs uv if there is a directed uv-path in the original graph. If the original digraph is acyclic, the transitive closure defines a partially ordered set.
Of more practical importance is the reverse construction principle: An arc uv is called transitive if there is a directed uv-path with intermediate nodes. The intransitiveReduction constructor omits all transitive arcs of the original digraph. Observe that this subgraph is well-defined only if the original digraph is acyclic and simple. The so-called Hasse diagram of a DAG is obtained by taking the intransitive reduction and computing a layered drawing of it.
The following shows a directd acyclic graph, with the red arcs forming its intransitive reduction:
[See API]
This addresses the methods which derive graph objects from two given input graphs. Actually, no new object is instanciated, but one graph is modified by means of the other. Two methods are available:
- abstractMixedGraph::AddGraphByNodes() is for node disjoint merge. The earlier figure - showing a primal-dual pair - has been built by first constructing the dual graph and then using this disjoint merge method.
- abstractMixedGraph::FacetIdentification() requires a planar target graph, and another graph with a simple eterior orbit. The latter is inserted into the target graph, into each face with a matching cardinality.
The facet identification method can be used to construct star solids from convex solids, and tilings (subdivisions of 2D grid graphs) as provided in earlier GOBLIN releases. This also includes the possibily of constructing non-planar graphs on a planar skeleton.
[See API]
Two constructor methods are provided which result in dense graph objects, whose edge length labels encode the node distances of the input graph:
- distanceGraph, which is defined for general input graphs, essentially a square distance matrix.
- metricGraph, which is defined for undirected input graphs only, essentially a triangular distance matrix.
There is also a sparse concept, voronoiDiagram, which takes a set of terminal nodes of the input graph, assigning the non-terminal nodes to the region of a nearest terminal. The Voronoi regions are the nodes of the new graph, and the edge lengths are the distances of the respective terminals.
[See API]
All graph objects with a sparse representation can be randomly augmented to disturb the incidence structure. All methods augment by a specified number of arcs, either without any restrictions, by a closed walk, or such that no node exceeds a given degree bound.
[See API]
After a graph object has been derived from another data object, and computations have been done on the derived graph instance, it is often required to map back the computational results to the original graph. For this goal, two methods abstractMixedGraph::OriginalOfNode() and abstractMixedGraph::OriginalOfArc() are provided.
There is no global rule of what the index returned by abstractMixedGraph::OriginalOfNode(v) represents. It may be a node index, an arc index with or without the arc direction bit or any other entity which can be addressed by an index.
Backtransformations are maintained only if abstractMixedGraph::OPT_MAPPINGS is specified to the respective constructor method. Not all concrete classes support this feature at the time!
[See API]
Return to main page