Connectivity and minimum cuts

Minimum Cuts

In the standard setting, a minimum edge cut denotes a node set bipartition of an undirected graph such that a minimum multiplicity sum of the edges with end nodes in different parts results. The library also deals with a couple of problem variations:

• The directed setting, better: The general setting of mixed graphs. Only those directed arcs count which are unblocking from the left-hand to the right-hand side.
• The setting where a left-hand node and / or a right-hand node are fixed
• The setting with restricted node capacities (abstractMixedGraph::NodeConnectivity() and abstractMixedGraph::StrongNodeConnectivity()). If all node capacities are virtually infinite, this is the same as computing edge cuts.

To all methods, the upper capacity bounds apply as the edge multiplicities and, for the methods dealing with restricted node capacities, the node demands are interpreted as the node capacities.

The derived cuts a exported by the node colour register with the following interpretation:

• Colour index 0 stand for cut nodes
• Colour index 1 stand for left-hand nodes
• Colour index 2 stand for right-hand nodes

[See API]

Connected components

Given a fixed connectivity number and characteristic, one might be interested in a connectivity test and maximal connected subgraphs.

For the edge connectivity and the strong edge connectivity case, the library includes methods to partition the node set such that all partial induced subgraphs are maximally connected. These methods formally return whether the graph object is connected and, if not, export the connected components by the node colour register. The respective codes for 1-edge connectivity, 2-edge connectivity and strong 1-edge connectivity run in linear time. The codes for high connectivity orders iterate on the min-cut methods, and hence are polynomial but not really efficient.

Concerning vertex connectivity, a partition into edge disjoint blocks is possible (and implemented) only in the low order cases: For 1-connectivity and strong 1-connectivity, the respective edge connectivity methods apply. The depth-first search method abstractMixedGraph::CutNodes() returns the 2-blocks (the edge-disjoint, maximal biconnected subgraphs) by the edge colour register, and the cut nodes by the node colour register. This procedure

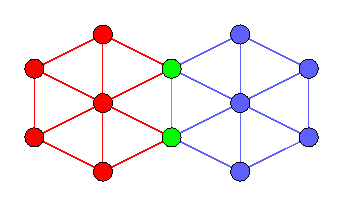
Starting with k=3, the maximal k-connected subgraphs (called k-blocks) are in general not edge disjoint as the following graph illustrates:

Herein, the green nodes form a cutting pair, and the green edge is contained in both 3-blocks. There is the concept of SPQR-trees to represent the 3-blocks, but this is out of the library scope.

[See API]

Planar connectivity augmentation

Especially planar drawing algorithms depend on certain connectivity levels of the input graph. To meet these requirements, the library contains methods to augment planar represented graphs such that the resulting graph is also planar, the derived planar representation can be reduced to the original planar representation and the ouput is connected.

Here are some caveats:

• The methods do not apply to general (non-planar) graphs
• The methods do not even apply to implicitly planar graphs, only when a planar representation is at hand
• The augmentation methods also require a certain level of connectivity. That is, abstractMixedGraph::Triangulation() requires a biconnected planar graph, and abstractMixedGraph::PlanarBiconnectivityAugmentation() requires a connected graph.
• Both methods do not derive minimal augmentations, and do not even achieve a fixed approxiation ratio. Even if each single augmentation step would be optimal, step-by-step application would not.

Although the library code is very elaborate, there are also theoretical limitations: The planar biconnectivity augmentation problem is NP-hard. For the planar triconnectivity augmentation of biconnected graphs, it is not even known if a polynomial time method is possible.

Dropping the planarity requirement admits linear time augmentation methods, but no such library code is available.

[See API]

Return to main page